An introduction to wireless transmission.

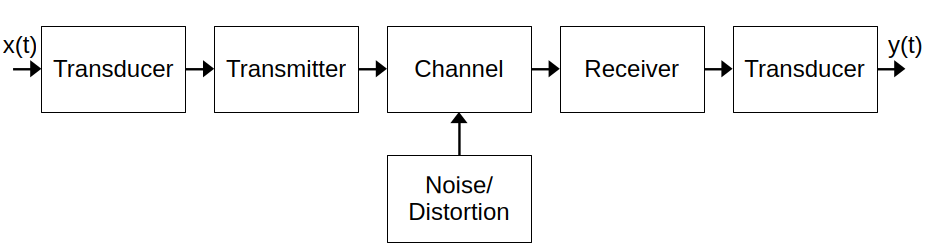
1. High Level Focus of Study

The course focuses on transmitter and receiver design, with an emphasis on dealing with channel and distortion effects.

2. Channel Characteristics

Given a channel of bandwidth B with noise so that the transmitter signal has a signal-to-noise ration of SNR, the channel capacity C (bits/sec = baud rate) is given by:

$$C=Blog_2(1+SNR)$$

At low SNR, the improvement in C seems linear, until SNR gets large and return on investment dips.

3. Modulation

Modulation is the process of translating the message signal into a form that allows efficient transmission over a channel.

3.1 Motivation

The main purpose of modulating signals is to bring the signal up to a higher frequency band - to understand why this is valuable, consider the length of the antenna required to transmit a signal of frequency $f$. The signal is transmitted as an electromagnetic wave, with wavelength $\lambda$ given by

$$\lambda=\frac{c}{f}=\frac{3\cdot 10^8}{f}$$

.

A fundamental result from studying electromagnetism is that the dipole antenna structure resonates at wavelengths that obey the following relationship, with $L$ being the length of the antenna:

$$L=n\frac{\lambda}{4}, \forall n = 1,2,3...$$

However, most signals that we wish to transmit require huge antennae lengths - for example, the human voice operates just up to about $f=6kHz$ or so. This requires an antenna length of AT LEAST 12.5 km!

Antennae of this size are not only impractical to construct and operate - they also have such high parasitic losses that it would be extremely hard to properly power. Therefore, if we could move the “baseband” signal up to a higher frequency, we could make practical, efficient antennas. An extra bonus is the ability to separate signals that are transmitted at the same time from one another - we can allocate different frequency bands for different uses, allowing anyone to tune into any given band at any time to receive or transmit on that band… provided they have permission/licensing.

3.2 The Modulation Property of the Fourier Transform

Recall from signals and systems:

$$\mathcal{F}\{x(t)cos(2\pi f_ct)\}=\frac{1}{2}\mathcal{F}\{x(t)(e^{j2\pi f_c t} + e^{-2\pi f_c t})\}=\frac{1}{2}X(f)*(\delta(f+f_c) + \delta(f-f_c))=\frac{1}{2}(X(f+f_c) + X(f-f_c))$$

This allows us to modulate signals.

3.3 Sine Waves as a Choice for Modulation

It is important to examine the prevalence of multiplication by the sine wave for modulation. Indeed, it seems that any high frequency periodic signal could give us a modulated signal (by the fourier series), so why sine waves in particular?

1. Frequency is invariant to linear systems
2. Generation of sinusoids is easy
3. Sinusoids take up minimal bandwidth themselves.

4 Going Forward

There are two types of analog modulation that will be discussed in this course:

• Amplitude Modulation
• Frequency Modulation