Bar-Spring-Problem
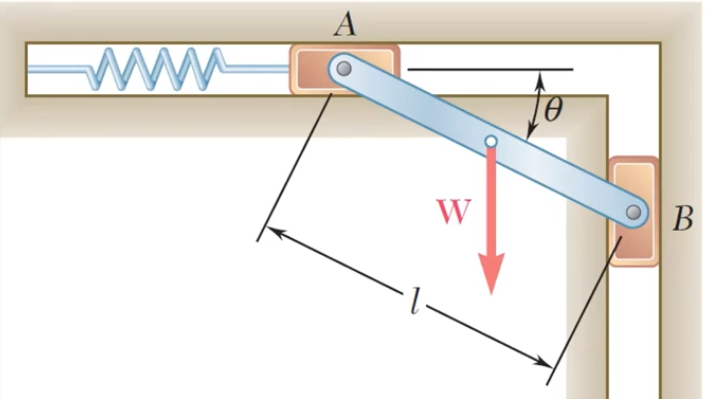
Determine $\theta$ when the system reaches equilibrium. $\theta = 0$ when the spring is uncompressed.
Notice that
$$F_s = k\Delta x = k[l-lcos(\theta)]=kl[1-cos(\theta)]$$Now, apply static equilibrium:
$$\Sigma F_x=0=B_x-F_s \Rightarrow B_x=F_s$$$$\Sigma F_y=0=A_y-w \Rightarrow A_y=w$$
$$\Sigma M_A=0=w\frac{l}{2}cos(\theta)-F_slsin(\theta)$$
Substitute the expression that we found for $F_s$,
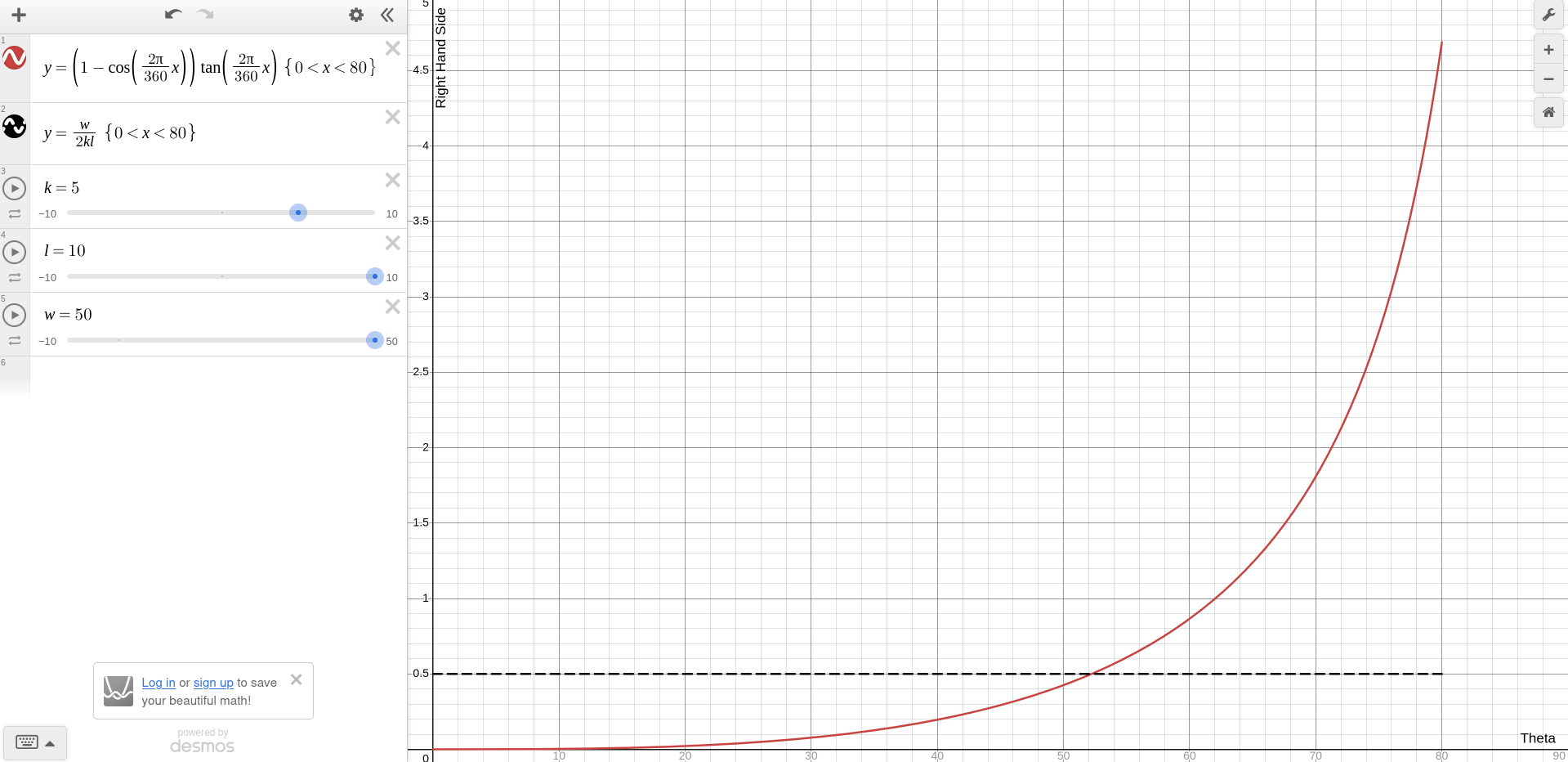
$$w\frac{1}{2}cos(\theta)=kl[1-cos(\theta)]sin(\theta)$$$$\frac{w}{2kl}=[1-cos(\theta)]tan(\theta)$$
Now we can use graphical methods to solve, using the factor $\frac{2\pi}{360}$ to convert the x-axis to degrees:za